CS 61B | Part 9 | Tree and Graph Traversals (DFS / BFS)

Tree Traversal

A tree consists of:

• A set of nodes.
• A set of edges that connect those nodes.
  • Constraint: There is an exactly one path between any two nodes.

Trees are a more general concept.

• Organization charts
• Family lineages
• File system trees

Sometimes you want to iterate over a tree. For example, suppose you want to find the total size of all files in a folder.

• What one might call tree iteration is preferably called tree traversal.
• Unlike lists, there are many orders in which we might visit the nodes. Each ordering is useful in different ways.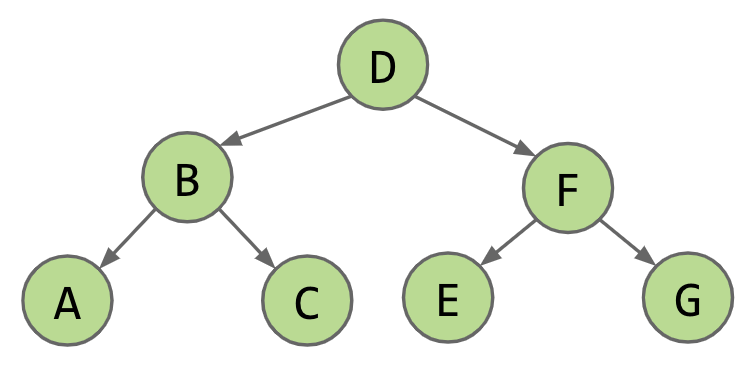
  
  • Level Order: DBFACEG
  • Depth First Traversals (DFS):
    • Pre-order: Visit the node, then traverse its children. DBACFEG

      preOrder(BSTNode x) {
        if (x == null) return;
        print(x.key);
        preOrder(x.left);
        preOrder(x.right);
      }

    • In-order: Traverse left child, visit the node, then traverse right child. ABCDEFG

      inOrder(BSTNode x) {
        if (x == null) return;
        inOrder(x.left);
        print(x.key);
        inOrder(x.right);
      }

    • Post-order: Traverse left child, traverse right child, then visit the node. ACBEGFD

      postOrder(BSTNode x) {
        postOrder(x.left);
        postOrder(x.right);
        print(x.key);
      }

Pre-order and post-order generalize naturally to trees with arbitrary numbers of children. However, in-order only makes sense for binary trees.

What Good Are All These Traversals?

Pre-order:

Post-order:

Graphs

Definition

A graph consists of:

• A set of nodes.
• A set of zero or more edges, each of which connects two nodes.

A simple graph (vs. multigraphs) is a graph with:

• No Loops: No edges that connect a vertex to itself.
• No Parallel Edges: No two edges that connect the same vertices.

Note: Trees are also graphs, but not all graphs are trees.

Since simple graph is more often in usage. In 61B, all graphs will be simple and we call them just “graphs” rather than “simple graphs”.

Graph Types:

More Graph Terminology:

Note that the length of a path is determined by the number of edges.

Graph Problems

There are lots of interesting questions we can ask about a graph:

• What is the shortest route from $S$ to $T$? What is the longest without cycles?
• Are there cycles?
• Is there a tour that only uses each node exactly once?
• Is there a tour that only uses each edge exactly once?

More Queries More Theoretically:

• S-T Path: Is there a path between vertices $S$ and $T$?
• Connectivity: Is the graph connected, i.e. is there a path between all vertices?
• Biconnectivity: Is there a vertex whose removal disconnects the graph?
• Shortest S-T Path: What is the shortest path between vertices $S$ and $T$?
• Cycle Detection: Does the graph contain any cycles?
• Euler Tour: Is there a cycle that uses every edge exactly once?
• Hamilton Tour: Is there a cycle that uses every vertex exactly once?
• Planarity: Can you draw the graph on paper with no crossing edges?
• Isomorphism: Are two graphs isomorphic (the same graph in disguise)?

Often can’t tell how difficult a graph problem is without very deep consideration.

Some well-known graphs problems: Euler Tour and Hamilton Tour. An efficient Euler tour algorithm $O(\text{number of edges})$ was found as early as 1873. Despite decades of intense study, no efficient algorithm for a Hamilton tour exists. Best algorithms are exponential time.

S-T Connectivity

Given a source vertex $S$ and a target vertex $T$, is there a path between $S$ and $T$?

It is an algorithm based on DFS.

boolean isConnected(Node s, Node t) {
  mark(s); // visit
  if (s == t) { // consider the base case! Only one vertex.
    return true;
  }
  for v in neighbors(s) {
    // recursive call
    if (!isMarked(v) && isConnected(v, t)) {
      return true;
    }
  }
  return false;
}

Follow the example in these slides to see how.

Traversal: DFS

The idea of exploring a neighbor's entire subgraph before moving on to the next neighbor is known as Depth First Traversal/Search. It is called “depth first” because you go as deep as possible.

Explore $1$’s subgraph completely before using the edge $0-3$.

DFS is not good for date preparation (why).

DFS is a very powerful technique that can be used for many types of graph problems.

Let’s discuss an algorithm that computes a path to every vertex. (DepthFirstPaths)

DepthFirstPaths Demo:

Demo: link (important)

We just developed a depth-first traversal (like pre-order, in-order, post-order) but for graphs.

Intuitively, we’re going deep (i.e., down our family tree to our first child, our first child’s first child a.k.a. our first grandchild, our first grandchild’s first child, and so on… visiting this entire lineage), before we even touch our second child.

Example:

Traversal: BFS

Note: BFS pseudocode is exactly the same as DFS except with a queue instead of a stack.

BFS has the cool feature of finding the shortest path from one node to all other nodes in terms of number of edges.

Demo: Breadth First Paths

Example: The Oracle of Bacon

API: Integer Vertices

Our choices can have profound implications on:

• Runtime.
• Memory usage.
• Difficulty of implementing various graph algorithms.

For example, using a map to store labels / weights (String to Integer):

Graph API:

Some features:

• Number of vertices $V$ must be specified in advance.
• Does not support weights (labels) on nodes or edges.
• Has no method for getting the number of edges for a vertex (i.e. its degree).
  • adj(int v).size() does the work.

// return the degree of a vertex
public static int degree(Graph G, int v) {
  int degree = 0;
  for (int w : G.adj(v)) {
    degree += 1;
  }
  return degree;
  // or just return G.adj(v).size()
}

Try to write a client method called print that prints out a graph.

// print all edges of a graph
public static void print(Graph G) {
  // for each vertex v
  for (int v = 0; v < G.V(); v += 1) {
    // for each neighbor w of the vertex v
    for (int w : G.adj(v)) { // Iterable
      System.out.println(v + " - " + w);
    }
  }
}

The runtime is $O(V + E)$. The first loop takes $O(V)$ since each vertex is visited once; the print statement takes $O(E)$ in total.

So, our choice of Graph API has deep implications on the implementation of DFS, BFS, print, and other graph “clients”.

Graph Representations

Adjacency Matrix

G.adj(2) would return an iterator where we can call next() up to two times:

• returns $1$
• returns $3$

Total runtime to iterate over all neighbors of $v$ is $\Theta(V)$. Underlying code has to iterate through entire array to handle next() and hasNext() calls.

So the print() takes $\Theta(V^2)$ time. Again, the inner loop takes $O(V)$ time because each vertex is visited.

Edge Sets

So the print() takes $O(E)$ time.

Adjacency Lists

So what is the runtime of print()?

The answer:

Best case: $O(V)$
Worst case: $O(V^2)$

Note: They can be expressed as $O(V + E)$.

Examples:

• Sparse Graph: Where $E$ grows very slowly, e.g. every vertex is connected to its square: 2 - 4, 3 - 9, 4 - 16, 5 - 25, etc.
  • $E$ is $\Theta(sqrt(V))$. Runtime is $\Theta(V + sqrt(V))$, which is just $\Theta(V)$.
• Dense Graph: Where $E$ grows very quickly, e.g. every vertex connected to every other.
  • $E$ is $\Theta(V^2)$. Runtime is $\Theta(V + V^2)$, which is just $\Theta(V^2)$.

Best case:
Each vertex has 2 or 0 edges. So the inner loop takes constant time.
A ------ B        A       B
|        |
|        |   OR  
|        |
C ------ D        C       D

Worst case (fully connected):
Each vertex has (V - 1) edges. So the inner loop takes ~V time.
A ------ B
| \    / |
|   \    |
| /   \  |
C ------ D

Explanation:

for (int v = 0; v < G.V(); v += 1) { // V times
  for (int w : G.adj(v) { // Cost model: next()
    System.out.println(v + " - " + w); // # next() = # println
  }
}

The total times (we don’t know the times in each loop) of calling next() is $2E$, not relevant to number of vertices $V$. So in total we have $O(2E)$.

Additionally, each loop we have to call G.adj(v) or v += 1, which in total takes $O(V)$.

Therefore, the runtime is $O(V + E)$.

Summary:

Note: print() and hasEdge(s, t) operations are not part of the Graph class’s API.

In practice, adjacency lists are most common.

• Many graph algorithms rely heavily on adj(s).
• Most graphs are sparse (not many edges in each bucket).

Bare-Bones Undirected Graph Implementation:

public class Graph {
  private final int V;
  private List<Integer>[] adj;

  public Graph(int V) {
    this.V = V;
    adj = (List<Integer>[]) new ArrayList[V];
    for (int i = 0; i < V; i += 1) {
      adj[i] = new ArrayList<>();
    }
  }

  public void addEdge(int v, int w) {
    adj[v].add(w);  adj[w].add(v);
  }

  public Iterable<Integer> adj(int v) {
    return adj[v];
  }
}

Code: DFS

Note: Check mark before DFS. (Both DFS and BFS require checking when iterating neighbors)
Note: Mark when visited or at the beginning of DFS or before looping.
Note: Update edgeTo after checking and before dfs() when iterating. (Need the information of the previous vertex)
Note: Output when doing dfs() or popping from the stack (not marked). Additionally, in post-order, output should be placed in the end of dfs().

Common Design of Graph Problems:

Common design pattern in graph algorithms: Decouple type from processing algorithm.

• Create a graph object.
• Pass the graph to a graph-processing method (or constructor) in a client class.
• Query the client class for information.

Paths P = new Paths(G, 0); // source is vertex 0
P.hasPathTo(3); // returns true
P.pathTo(3); returns {0, 1, 4, 3}

Constructor & dfs(Graph G, int v):

Iteration Version:

// Using a stack
Initialize the stack;
  push the starting vertex on the stack;
  while stack is not empty:
    pop a vertex off the stack;
    if vertex is not marked:
      // since the stack may contain same nodes
      // then it is safe to visit!
      mark the vertex; // mark when visited or before loop
      visit the vertex; // edgeTo couldn't be here
      for each neighbor of vertex:
        if the neighbor is not marked: // check mark before dfs
          // update edgeTo[neighbor] = vertex
          push the neighbor to stack.

Note however that DFS and BFS differ in more than just their fringe data structure. They differ in the order of marking nodes:

• Mark When Visiting/Popping: For DFS, we mark nodes only once we visit a node (a.k.a. pop it from the stack). As a result, it’s possible to have multiple instances of the same node on the stack at a time if that node has been queued but not visited yet.
• Mark When Enqueuing: For BFS, we mark nodes as soon as we add them to the fringe so that the above situation is not possible.

pathTo(int v) & hasPathTo(int v):

What is the runtime of the constructor?

Refer to the demo for visualization: Demo

• The number of if (!marked[w]) calls is $\sim{2E}$.
• The number of dfs() calls is $V$.

Note that just similar to the print() runtime, whose outer loop takes $V$ times, here we count how many times we call dfs(). We call dfs() when the vertex is not marked, so it should be $V$ times. It’s very important!

private void dfs(Graph G, int v) {
  marked[v] = true;
  int[] ns = adj[v]; // O(1), or using the call G.adj(v)
  // how many times we call dfs() * O(1) = O(V)
  for (int w = 0; w < ns.length; w += 1) {
    if (!marked[w]) { // O(1), or using the call next(). In total, 2E times.
      // ...
    }
  }

So the runtime is $O(V + E)$.

• Each vertex is visited (being an active vertex) at most once ($O(V)$).
• Each edge is considered at most twice ($O(2E)$).
  • Maybe some are not reachable.

We can’t just use only one cost model like marked[w]. Consider the case that there are no vertices and it still takes $O(V)$ time because each vertex is checked.

Note: Can’t say $\Theta(V + E)$, e.g. graph with no edges touching source.

Space is $\Theta(V)$. Need arrays of length $V$ to store information.

Code: BFS

Note: Check mark before enqueued (after forlooping neighbors).
Note: Mark when enqueued.
Note: Update edgeTo after checking and when enqueued (in forlooping).
Note: Output when dequeued.

Notice that after dequeuing a vertex we don’t check if it is marked, because according to mark when enqueuing the vertex must have been marked.

Cost model:

• dequeue() or G.adj(v)
• if (!marked[w]) checks or next()

What happens if we use adjacency matrix?

It takes $O(V^2)$.

Ex (Guide)

Tree Traversal

Ex 1 (Pre-order = In-order)

Question 1 from the Fall 2014 discussion worksheet.

Pre-order: 10, 2, 5, 7, 8, 3, 0, 2
In-order: 5, 2, 7, 8, 10, 3, 0, 2
Post-order: 5, 8, 7, 2, 2, 0, 3, 10

Bonus: The height in this case is $N - 1$ (I think the answer is incorrect). It means all nodes have only right children.

Height is the number of edges along the path. And this is the version used in CS 61B.

Source: link

Ex 2 (Diameter)

Very interesting!

Question 4 from the Fall 2014 midterm.

The diameter of a tree (for this problem, a binary tree) is the maximum number of edges on any path connecting two nodes of the tree. For example, here are two sample trees and their diameters. Also, the nodes along the longest path are starred.

Draw a graph with small cases to get intuition!

Note:

• The diameter of an empty tree or a tree with one node is $0$.
• height(null) returns -1.

(The code in the picture is not correct.)

Idea: Assume we have a current node x. Its left subtree’s diameter is l and its right subtree’s diameter is r. Note that the left child or the right child need not to be the connecting node along the longest path. For example, in the above 2nd tree, assuming A is a left child of a tree, the A node itself is not along the longest path.

When connecting x to its two subtrees, is it possible that x as a connecting node generating a longer list whose height is l + r + 2? (Consider subtree is null).

Since x‘s left or right child might not be the connecting node, we cannot use their maximum diameters instead of their maximum heights.

// postorder style - O(N)
private static int height(BinTree T) {
  if (T == null) {
    return -1;
  }
  return Math.max(height(T.left), height(T.right)) + 1;
}

public static int diameter(BinTree T) {
  // Base Case: T == null OR T has no children => 0
  if (T == null) {
    return 0; // remember: number of edges!
  }
  if (T.left == null && T.right == null) {
    return 0;
  }
  int leftResult = diameter(T.left); // postorder
  int rightResult = diameter(T.right);
  int childBest = Math.max(leftResult, rightResult);
  /*
     O               O               O
    / \             /
   O   O           O
   0 + 0 + 2 = 2  0 + -1 + 2 = 1   -1 + -1 + 2 = 0
  */
  int currBest = height(T.left) + height(T.right) + 2;
  // connecting the current node T - O(N)
  return Math.max(childBest, currBest);
}

Time:

• Best: $O(N\log{N})$
• Worst: $O(N^2)$

Space:

• Best: $O(\log{N})$
• Worst: $O(N)$

Ex 3 (Drawing)

Question 7 from the guerrilla section worksheet #2 from Spring 2015.

(a) Draw a full binary tree that has a pre-order of $C, T, U, W, X, S, A, Z, O$ and a post-order of $W, X, U, S, T, Z, O, A, C$. Each node should contain exactly one letter.

(b) What is the in-order of this tree?

In-order: $W, U, X, T, S, C, Z, A, O$

C level

Ex 1 (BFS)

Problem 2a from Princeton’s Fall 2009.

List the vertices in the order in which the vertices are enqueued on the FIFO queue. (BFS)

A B C D G E F I H

Ex 2 (Shortest?)

Suppose we run BFS from a vertex $s$. The edgeTo[] array we get back is sometimes known as a “Breadth First Search Tree”. What, if anything, does the BFS tree tell us about the shortest path $(v,w)$ from $v$ to $w$, assuming that neither is the source?

Conclusion:

$(s,v)$ and $(s,w)$ are the shortest paths.

If $v$ is on the path $(s, w)$, $(v, w)$ is the shortest path from $v$ to $w$.

$$(s,w) = (s,v) + (v,w)$$

Contradiction:

Assume $(v,w)$ is not the shortest path. So there has to be a shorter path $(v,w)’$ which is shorter than $(v,w)$. Then we have:

$$(s,v) + (v,w)’ = (s,w)’ < (s,v) + (v,w) = (s,w)$$

There is a shorter path $(s,w)’$ between $s$ and $w$, which contradicts the condition that $(s,w)$ is the shortest one.

Ex 3 (DFS Pre & Post)

Problem 3a from Princeton’s Fall 2010 final.

Pre-order: A B G D F C E H I
Post-order: G B E C I H F D A

Pre-order: A B G C D F E H I
Post-order: G B E I H F D C A

B level

Ex 1 (BFS Simultaneous)

Problem 2b from Princeton’s Fall 2009 final.

The answer is (d). I don’t know why II is correct.

Ex 2 (Application)

Problem 1c from Princeton’s Spring 2008 final.

Application:

• BFS: Shortest path (fewest number of edges) from $s$ to $t$.
• DFS: Topological sort, strongly connected components, Euler tour.

Ex 3 (DFS Simultaneous)

Problem 3b from Princeton’s Fall 2010 final.

The function-call stack always contains a sequence of vertices on a directed path from $s$ to current vertex (with $s$ at the bottom and the current vertex at the top).

I, II

What if I pop s and push x and y?
x
/
s

y
Don’t understand why II must be true.

Ex 4 (Bipartite Graphs)

Problems 4 from Spring 2016’s discussion worksheet.

An undirected graph is said to be bipartite if all of its vertices can be divided into two disjoint sets $U$ and $V$ such that every edge connects an item in $U$ to an item in $V$. For example, the graph on the right is bipartite, whereas on the graph on the left is not. Provide an algorithm which determines whether or not a graph is bipartite. What is the runtime of your algorithm?

To solve this problem, we simply run a special version of DFS or BFS from any vertex. This special version marks the start vertex with a $U$, then each of its children with a $V$, and each of their children with a $U$, and so forth.

If any vertex already has a $U$ and the visited vertex has a $V$ (or vice-versa), then the graph is not bipartite. In other words, if any vertex which is marked $U$ finds a neighbor which is already marked $U$, break, and the graph is not bipartite.

If the algorithm completes, marking every vertex in the graph, then it is bipartite.

If the graph is not connected, we repeat this process for each connected component.

Note: If a graph $G$ is bipartite, then it cannot contain an odd cycle.

Consider the DFS tree:

Clab 9 (Party)

Guide: link
Code: Graph.java & SeparableEnemySolver.java

Need consider:

• Disconnected graph
• Divide into 2 groups
• Divide into 3 groups (optional)
  • When encounter V - V, we modify the target node to Q
  • When encounter Q - Q, we modify the source node to U
  • When encounter U - U, return false

Ex 5 (Shortest Directed Circle)

Problems 4 from Spring 2016’s discussion worksheet.

Provide an algorithm that finds the shortest directed cycle in a graph in $O(EV)$ time and $O(E)$ space, assuming $E > V$.

The key realization here is that the shortest directed cycle involving a particular source vertex is just some shortest path plus one edge back to $s$. Using this knowledge, we can create a shortestCycleFromSource(s) subroutine. This subroutine first runs BFS on $s$, then checks every edge in the graph to see if it points at $s$. For each such edge originating at vertex $v$, it computes the cycle length by adding one to distTo(x) (which was computed by BFS).

This subroutine takes $O(E +V)$ time because it is BFS. To find the shortest cycle in the entire graph, we simply call shortestCycleFromSource() for each vertex, resulting in an $V \times O(E + V) = O(EV + V^2)$ runtime. Since $E > V$, this is just $O(EV)$.

Ex 6 (sumDescendants)

Problem 4c from Hug’s Spring 2015 Midterm 2.

// Notice the class is TreeNode
public class TreeNode {
  public TreeNode left, right;
  public int value;

  public TreeNode(int n) {
    value = n;
  }

  /** Replaces value with sum of all of its descendants' values.
   *  Changed by sum of descendants
   *  Returns original value + sum of descendants
   */
  public int sumDescendants() {
    if (left == null && right == null) { // this is not null
      int oldVal = value;
      value = 0;
      return oldVal;
    }
    else {
      // ------ Bug: left or right is null -------
      // sumDescendants() returns the sum of original value + sum of descendants
      int sum = left.sumDescendants() + right.sumDescendants(); // 36 = 4 + (8) + 8 + (16)
      // -----------------------------------------
      
      int leftSum = 0;
      int rightSum = 0;

      if (left != null) {
        leftSum = left.sumDescendants();
      }
      if (right != null) {
        rightSum = right.sumDescendants();
      }

      int oldVal = value;
      value = leftSum + rightSum;
      return oldVal + value;
    }
  }
}

A level

Ex 1 (Eulerian tour)

Develop an algorithm that determines whether or not a directed graph contains an Eulerian Tour (Eulerian Path), i.e. a tour that visits every vertex exactly once.

• From GeeksforGeeks
• From GeeksforGeeks
• From StackExchange

Eulerian Path is a path in graph that visits every edge exactly once. Eulerian Circuit is an Eulerian Path which starts and ends on the same vertex.

A graph is called Eulerian if it has an Eulerian Cycle and called Semi-Eulerian if it has an Eulerian Path.

The problem is same as following question. “Is it possible to draw a given graph without lifting pencil from the paper and without tracing any of the edges more than once”.

Properties (Undirected Graph):

• Eulerian Cycle:
  • All vertices with non-zero degree are connected. (We don’t care about vertices with zero degree because they don’t belong to Eulerian Cycle or Path)
  • All vertices have even degree.
• Eulerian Path:
  • Same as the first condition of Eulerian Cycle.
  • If two vertices have odd degree and all other vertices have even degree.

Note that: Only one vertex with odd degree is not possible in an undirected graph (sum of all degrees is always even in an undirected graph).

Note that: A graph with no edges is considered Eulerian because there are no edges to traverse.

Properties (Directed Graph):

• Eulerian Cycle:
  • All vertices with nonzero degree belong to a single strongly connected component.
  • In degree and out degree of every vertex is same.
• Eulerian Path:
  • Same as the first condition of Eulerian Cycle.
  • There should be a single vertex in graph which has $D_{in} + 1 = D_{out}$ and another vertex which has $D_{in} = D_{out} + 1$.
  • Rest of vertices should have $D_{in} = D_{out}$.

We can detect singly connected component using Kosaraju's DFS based simple algorithm.

To compare $D_{in}$ and $D_{out}$ degree, we need to store $D_{in}$ and $D_{out}$ of every vertex. $D_{out}$ can be obtained by size of adjacency list. $D_{in}$ can be stored by creating an array of size equal to number of vertices.

Ex (Examprep 9)

Ex 1 (K-th Ancestor)

(a) Consider the Tree class below. Suppose we would like to write a method for this Tree class, getAncestor(int k, Node target). This method takes in an integer $k$ and a Node target, and returns the k-th ancestor of target in our tree (you may assume such an ancestor exists). You may also assume that $k >= 0$, that target != null, and that there are no cycles in our tree before we call this method.

(b) Give a bound on the runtime of getAncestor(int k, Node target) in the best and worst case in $\Theta(\cdot)$ notation in terms of $N$ and $k$, for a tree with $N$ nodes. How does our choice of list implementation on line 10 affect our runtime?

• Best case: When the root is the target. The runtime is $\Theta(1)$.
• Worst case: The tree is a complete tree or a list. We need to traverse the entire tree, so the runtime is $\Theta(N)$.

The answer: A LinkedList is optimal since we only add/remove from the end of the list. return list.get(list.sie() - 1 - k) takes $\Theta(k)$. The problem with ArrayList is the it has resizing penalties.

Ex 2 (Contact)

We’re going to make our own Contacts application! The application must perform two operations: addName(String name), which stores a new contact, and countPartial(String partial), which returns the number of contacts whose names begin with partial. Implement both of these methods in the Contacts class below. You may find the work already done in the private Node class, as well as the method charAt(int index) useful.

Code: link